Başlığa gel. Komplo teorici oldum çıktım. Beni az çok tanıdıysanız komplo teorilerine ve astrolojiye (iğnemi batırma fırsatımı kaçırmam) nasıl karşı durduğumu bilirsiniz. O zaman bu başlık ne, tıklama yemi mi? Asla. Ben sınırlı okuyucu sayımla barışık bir insanım. Etrafımızdaki dünyanın gizli düzenini matematikten başka bir şeyle açıklamam, bilimden şaşmam.
Şimdi söyleyeceğim tespit karşısında başta inkar ve daha sonra, öfke, pazarlık, depresyon kısmını atlayarak doğrudan kabullenmeye geçeceksiniz. Çünkü ortada yas tutmalık bir durum yok, ani bir aydınlanma karşısında olsa olsa göz yaşlarınızı tutamayabilirsiniz o kadar.
Dünyadaki ve hatta arttırıyorum evrendeki tüm verilerin bağlı olduğu matematiksel bir düzen var. İlluminativari konuşmak çok eğlenceli. Gel okuyucu gel.
Gerçek hayatta karşılaştığımız doğal ve sosyal verilere bakıldığında -şehirlerin nüfusları, nehirlerin uzunluğu, fatura meblağları, ülkelerin yüzölçümleri, hisse senetleri fiyatları, atom ağırlıkları, elektrik faturaları, şirket gelirleri, dağların yüksekliği, İstanbul apartman fiyatları, Instagram like sayıları bile- ilk basamaklarındaki rakamlarının nasıl dağılmasını beklersiniz? Rastgele, öyle değil mi? 1 ila 9 arasındaki tüm rakamların birbiriyle eşit şekilde dağılmasını, her birini (sayı kaç basamaklı olursa olsun) birinci basamakta görme ihtimalimizin yüzde 11,1 olduğunu düşünürsünüz. Bir sayı 1 ile de başlayabilir aynı olasılıkla 7 ile de, 8 ile de…
Ama hayır, gerçek hayat bize 1 ile başlayan sayıları, ezici çoğunlukla, yüzde 30 ile daha yaygın göreceğimizi söylüyor. 2 ve 3 rakamlarını görmemiz de olası ancak daha sonraki rakamları görme sıklığımız ciddi bir şekilde düşüyor. İnanması zor olsa da her rakamın bir sayının başına gelme sıklığını tablo olarak aşağıda görebilirsiniz.
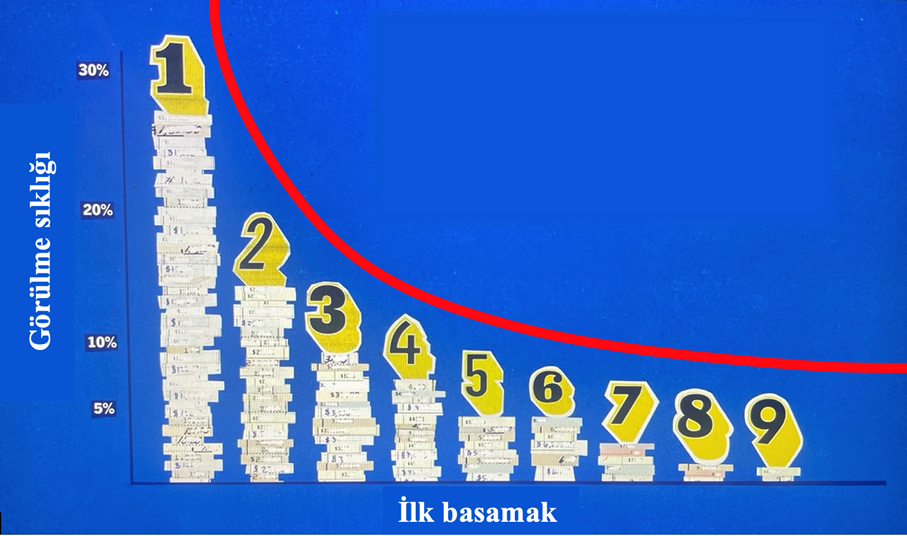
Enter, Frank Benford ve adını verdiği yasası: Benford Yasası. Benford, bu yasaya gazetelerden, atlaslardan, sokaklardan, spor karşılaşmalarından, akla gelebilecek her yerden topladığı 20 bin farklı veri setini inceleyerek vardı. Ondan 50 sene önce, 1881’de Simon Newcomb diye biri de bu düzeni fark etmiş ve incelemişti ama adını verecek kadar ününü yayamadıysa demek, ister istemez Benford ile anıyoruz bu yasayı.
Benford’un incelediği veri kaynaklarının çok önemli ortak yönleri vardı: Öncelikle geniş bir aralıktan gelen sayılar içermeli; köylerden metropollere kadar nüfuslar gibi. İkincisi, aldığınız örneklem binlerce ya da on binlerce sayı içermeli, yani 10.000 ayrı yerin nüfusu gibi. Üçüncüsü, sayılar sabit artışla değil, katlanarak büyümeli. Gerçek hayatta böyledir zaten. Müşteriler müşteri getirir, nehirler kol toplar uzar, ağaçtan ağaçlara yangın büyür, dedikodu ağızdan ağızlara yayılır.
Bu katlanarak büyüme işin sırrı, bu yüzden derin analize giriyoruz. Mesela gelirinin her ay yüzde 10 artışla büyümesi, bir başka deyişle gelirinin her ay 1,10 katlanması örneğine yakından bakalım. Benford Yasasının nasıl işlediğini bu tablonun gözler önüne sereceğini düşünüyorum. Her ay geliri 1,10 katına çıkaracağım ve çıkan sonucun ilk basamağındaki rakamı listeleyeceğim.
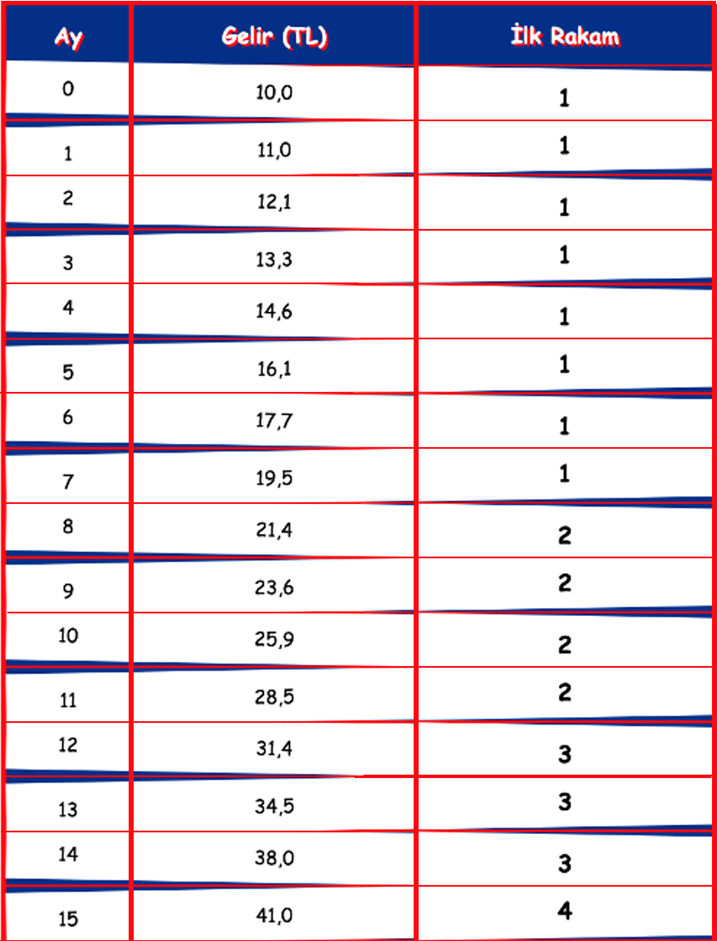
Tabloya baktınız. Şimdi bakın burası çokomelli. Gelirin 10’dan 20’ye çıkması için %100 artış lazım ve bu sekiz ay sürdü. Ama 20’den 30’a çıkması için %50 artış yeter, bu sadece dört ay aldı. 30’dan 40’a çıkmak için %33 artış yeter ve bu sadece üç ay aldı. Dikkat ettiyseniz ilk basamağın değişmesi için gereken artışa baktık (10’lardan, 20’lere, 30’lara...). Büyüme oranlarının 100-50-33 şeklinde yavaşladığını gördünüz. Doğada büyüme genellikle başta hızlı, sonra yavaşlayan bir yapıdadır. Ağaçlar ilk seneler hızlı uzar ama sonra uzamaları yavaşlar, öyle değil mi? Ya da ilk Instagram hesabı açtığınızda arkadaş sayınız hızla büyüme gösterir ama şimdi haftada kaç arkadaş ekleniyor? Bu doğaldır. İşte böyle doğal büyümelerde, 1’in ilk rakam olarak daha çok sahnede kaldığını fark ettiniz, yukarıdaki örnekte tam sekiz kez. Biz bu tabloda sekiz kez 1 rakamını sayıların başında gördük, dört kez ise 2 rakamını gördük.
Sevgili okuyucum, bir itiraf: Ben bu paragrafla Benford Yasasını anlatabilmek için üç saatimi harcadım. Siz de bu paragrafı üç kez okumaktan sakınmayın. Bu aydınlanmanın beyin hücrelerinizde çakacağı şimşeklerin faydası sporun vücudumuza faydasıyla eşdeğer. Bu tarz büyümelere verilen ad ‘logaritmik’ büyüme. Cümle içinde kullanın havanızdan geçilmez. Hele bu terimi liseli çocuklarla sohbette kullanırsanız derste ‘log’ alıp bu hayatımda ne işe yarayacak diye isyan eden gençleri dumur edersiniz.
Devam edecek olursak yasanın çalışması için, veri yapay kurallarla sınırlanmamış olmalı; TC kimlik numaralarının hepsi aynı uzunlukta olduğu için mesela burada yasa uygulanamaz. Ya da bilet numaraları gibi sabit aralıklarla artan şeyler olmamalı. En mühimi ise sayılar insanların kafasından uydurulmuş olmamalı.
Bu durumda size doğal diye yutturulmak istenen veri setlerinde sahtekarlık yapılıp yapılmadığını anlamak için elinizde sihirli bir değnek tutuyorsunuz. Kişi vergi mi kaçırıyor, seçimler manipüle mi edilmiş, hesap hareketlerinde tutarsızlık mı var, o influencer’ın milyonlarca takipçisi bot hesap mı? Influencer’ın takipçilerine bakın ve onların takipçi sayılarını sıralayın. Baktınız ki yüzde 30’u 1 ile başlamıyor, ya da 7, 8, 9’lar çok yaygın o zaman o takipçilerin bot olduğunu anlarsınız.
Enron 2000 yılında finansal verileriyle oynadı. Rakamları ne kadar çok gelirleri olduğunu göstermek için şişirmişlerdi. İşte bu skandal Benford Yasası kullanılarak bulundu. Enron verilerini bir grafiğe koydular ve yukarıdaki grafikteki kırmızı eğriye hiç uymadığını gördüler.
Kadim Benford Yasası her yerde ve her zaman bizimle ve matematiksel gerçekliğin sessiz tanığı olarak evrene hükmetmeye devam ediyor. Artık siz nedenini, nasılını biliyorsunuz. Ne dersiniz dünyayı yöneten beş büyük aileye alternatif yaratalım mı?